bead chain arch, appearing as white dots on a black background I am interested in shape, dynamics, and mechanics. Often this leads me to problems involving curved thin structures such as chains, strings, rods, membranes, plates, and shells. My group spends much of its time deriving and solving differential equations and playing in the lab. Much of our recent, current, and planned activity falls into one of the following overlapping areas: However, our interests are broader than this, the future is hard to predict, and by the time you are reading this the above descriptions are at least somewhat out of date. I am inspired by observation of many engineered structures and aspects of manufacturing related to materials processing, and welcome any excuse to apply geometric tools to nonlinear phenomena in classical continuum mechanics or soft condensed matter.
Here is an incomplete list of publications with some comments and informal errata. Other publications may be found on Google Scholar. I strongly recommend the arXiv versions of the linked articles, as the effects of journal publication often include mutilation of color, layout, and resolution of figures and equations, introduction of copyediting errors into equations and text, and other unfortunate events.
photo of bent blue sheet with two indentations
Transient and stable patterns and particle-like behavior of localized curvature.
Wading into this topic for the first time. A preliminary exercise, hoping to eventually relate two approaches (see below for long paper on pseudomomentum on which this is based).
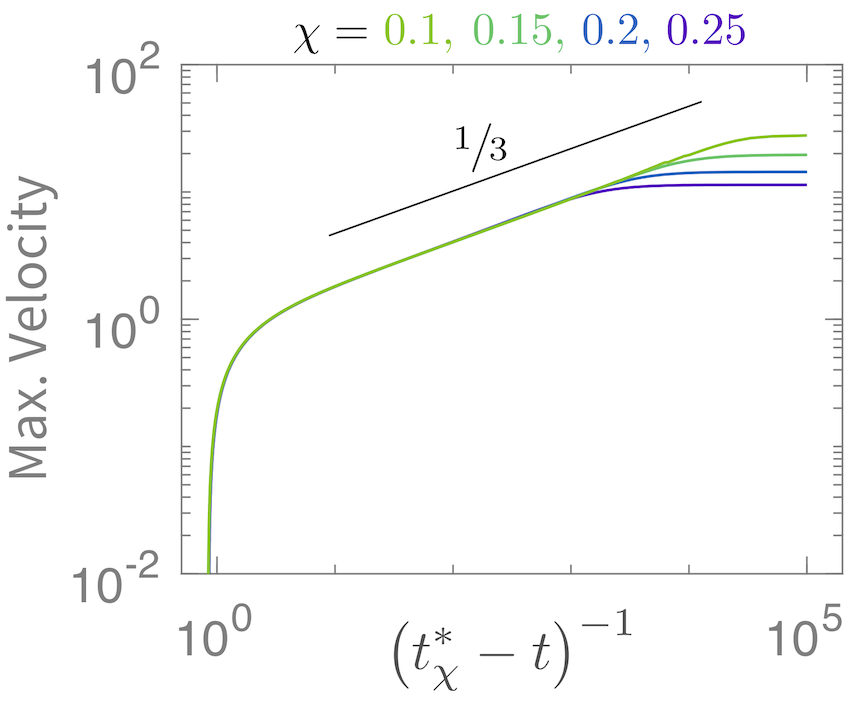
plot showing velocity scaling
The snapping (whipping, flapping) singularity and its regularization.
Two complementary routes to obtain primitive bending measures and energies for plates and shells. The plate measure is a generalization of an old result for straight rods, while the shell measure and its restriction to curved rods is entirely new. We compare with various commonly used models in soft matter, which all behave in qualitatively different ways.
A first stab at developing a systematic small-stretch elasticity theory, with an eye towards plate and shell theories.
trajectory curves
The first note on rigid body rotation started as a homework problem but got a bit more interesting. The follow up is a significant generalization in which we construct modifications to dynamical systems that selectively change their conserved quantities while retaining as much integrability as possible, driving the system towards nontrivial states.
folded blue plastic circles with holes
Exploring how the excision of singularities, creating virtual singularities, affects stiffness and multistability in sheets. In the case studied here, there is a curious re-entrant dependence on hole shape parameters.
stick model of helicoid
Plywood meets embeddings. A triumph of nominative determinism (see also bendy straw paper below).
Exploration of a balance law connected to material symmetry, with examples from elasticity, fluids, and structures. Corrects informal approaches in my previous papers.
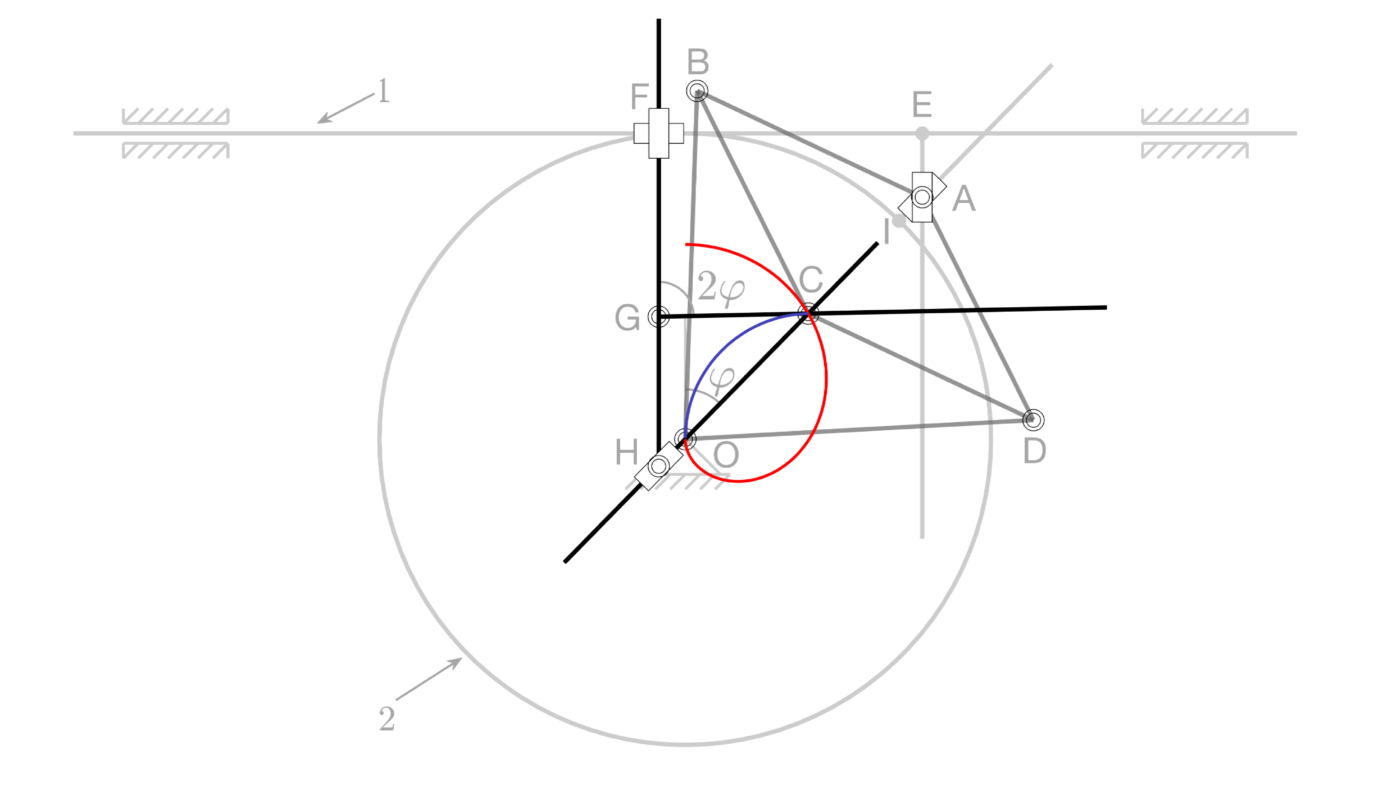
diagram of linkage mechanism
Cochleoids and other plane geometry relevant to studies of pleating, folding, creasing, and other forming operations.
A long paper resolving and raising some issues that have been bothering me for a while, and a short paper expanding a point from the long paper, in praise of Biot strains for thin structures (please note that the footnote mentioning neo-Hookean energy is half wrong).
pink pop toob bendy straw in front of OCCAM mug
A bendy straw, which can stably adopt just about any one-dimensional shape, only works because it's pre-stressed. Cut one length-wise and watch it relax to a larger radius. An incompatible four-bar linkage works similarly.
black and white bead chain coiling on a surface
A chain dropped onto a table falls faster than it would if the table were not there.
A classical approach to sleeve constraints, peeling, and similar problems.
curved blue plastic strip
curved blue plastic strip
Fun with SO(3). Multi-stability. Snapping movies. Unexpected problems with strip models.
An old problem revisited. Classification of elastica by momentum and pseudomomentum.
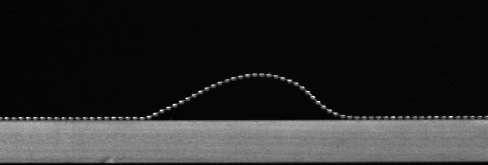
bead chain arch, grey on a black background
The paper is about contact discontinuities in extended bodies, particularly how the geometry depends on whether you are picking something up or laying it down. Examples include peeling tapes, moored structures, and some musical instruments. The video is an example of two propagating contact discontinuities.
colorful diagram
The classical catenaries are a one-parameter family of curves that don't change shape under translation and axial flow. Stick them in a fluid and they do, picking up four additional shape parameters. These solutions include towing, sedimentation, and other problems as subcases.
This note is about a constant arising in dynamical equilibria of thin bodies, which we later learned is related to the Eshelby tensor and to conservation of Kelvin circulation (we now realize that our comparison with the Bernoulli equation is misleading, as it relied on specifics of this problem, and is not generally correct). We also use symmetry arguments to provide the solutions for rotating, flowing strings, such as the steady state of a piece of unspooling yarn.
orange dancing tube airdancer
Phenomena such as kinks, shocks, partial contact, cracking, tearing, and cutting of thin structures involve propagating discontinuities in geometry or applied forces. This was my first clumsy attempt to understand these things in terms of action principles for non-material volumes. Some aspects of the approach probably need correction before it can be extended.
light grey sphere with blue shape in front
Here we examine the rotation of a flowing, flexible membrane. We find that a minimal model of metrically constrained dynamics generates peaked waves, just like this physical process.
grey shape with black grid
In a sheet of paper, a cone is a monopole: a point singularity in intrinsic curvature. So what's a dipole? There are actually two kinds.
At the free end of a moving string, the stress has to vanish, and a result is that the motion of the end is nontrivial.
These are the three-dimensional "jumpropica" or rigidly rotating strings, generalizing the known planar curves.
Take a pile of chain or rope sitting on a surface, and pull one end really fast. A strange arch-like feature appears. Our paper talks about several interesting issues that came up while we thought about this problem, though these are not necessarily the most important effects behind the arch and related phenomena such as the "chain fountain", about which open questions remain.
red dots on black ruffled shape
rolled up green and light green shape
  • Thermally responsive rolling of thin gel strips with discrete variations in swelling
    Kim, Hanna, Hayward, Santangelo
    sorry, no arXiv ｜ Soft Matter 8 (8) 2375-2381 (2012)
Adventures in making 3D curved surfaces by swelling flat 2D sheets.
drum shape, orange and green and yellow
The original draft had a better title, which you can still see thanks to the arXiv.